River cross-section analysis

Introduction

The purpose of this notebook is to look up at the hydraulic parameter at a specific cross-section. Especially to compute the potential elevation of water and the velocity in order to pre-design protection work such as dike or rip rap. These basic computations may be done also into spreadsheet. However, the second goals of this notebook is to become familiar with the "R" programming language, starting with a simple example.

Hydraulic considerations

Here we will use the so-called Manning-Strickler formula. It is basically the same than the Chézy's formula, but being more accurate due to higher exponent applied to the hydraulic radius (assumed to be better constrained, than the roughness coefficient). It is used worldwide and therefore produce a large amount of supporting documents. The difference between Manning and Strickler is in the way the roughness coefficient is expressed. The Manning coefficient is named "n" and the Strickler one is named "K_s". Their are related trough:

\( n = \frac{1}{K_{s}}\)

As it is very difficult getting reasonable guess of the value of the rougness coefficient in the area influenced only by the bed (as you often couldn't oberve it), one could you the following workflow. Although a little more complex than a direct approach, it avoids having to guess this partial roughness in the flow center line (the one on the banks is easier to calibrate because it can be observed directly).

In [ ]:

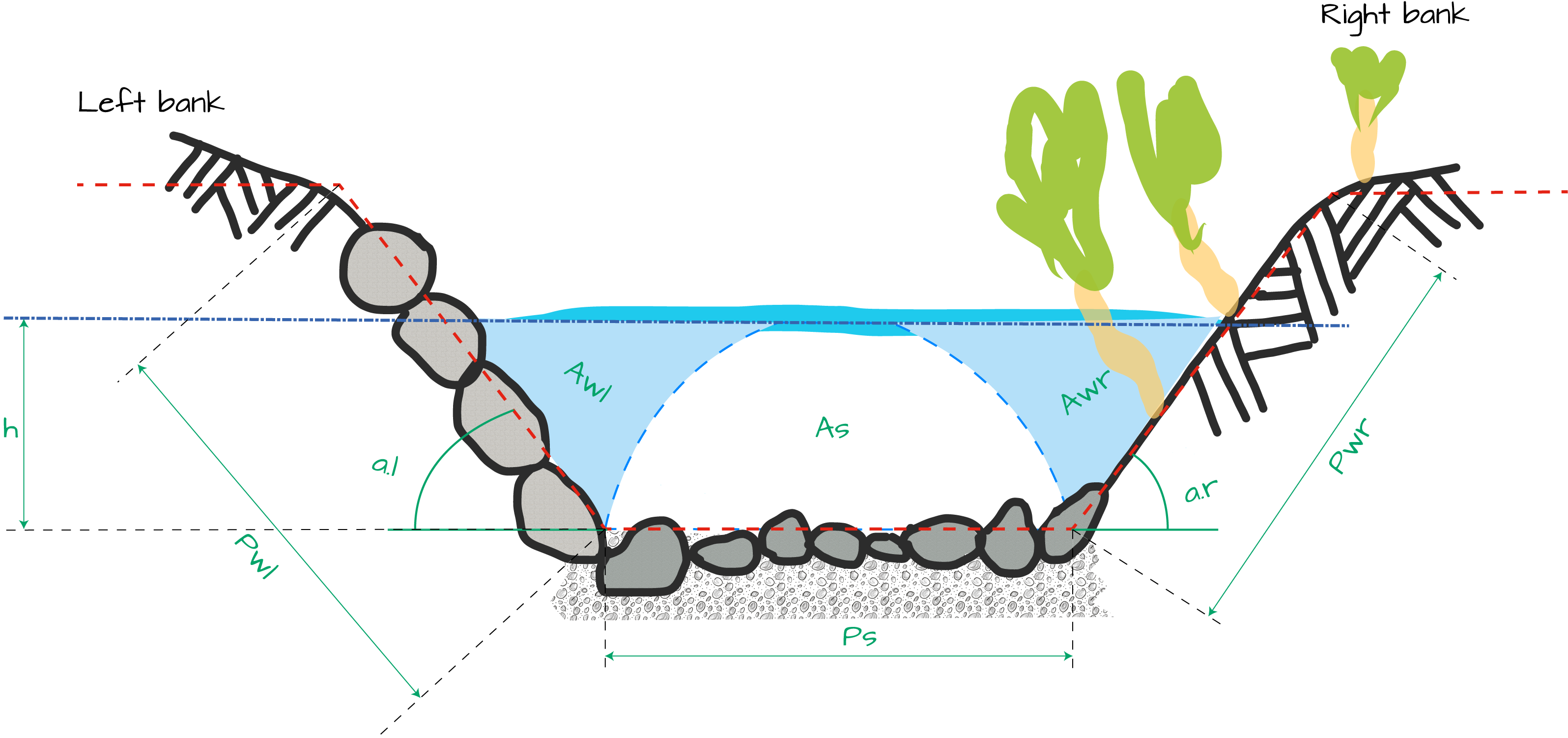
## Geometry description
Based on your field assessment of:
**n** the roughness coefficient (unit is **dimensionless**, see below)
**A** the equivalent trapezoidal section A = A<sub>wl</sub> + A<sub>s</sub> + A<sub>wr</sub> (unit is **m<sup>2</sup>**)
**P<sub>s</sub>** the wetted perimeter in the section influenced inly by the bed (= bed width in **m**)
**J** the longitudinal gradient of the river at this cross-section (unit is **m/m**, *i.e* an angle in radian)
**d<sub>90</sub>** the diameter of the equivalent sand roughness

Once these values are known (A is expressed as un function of water depth h) the following workflow may be applied for assessing the flow elevation at this cross-section. But first of all you should declare the known variables:

Variable initalisation

In [ ]:

#################################################
#######    Cross-section computation    #########
##########        26.01.2022       ##############
##########       by E. Bardou      ##############
#################################################

# 1. Initialization of variables
g <- 9.81 # terrestrial acceleration [m/s²]
J <- 0.003 # slope [m/m]
Ps <- 20 # wetted perimeter of the bottom, corresponds to the width of the bed, also sometimes called B [m]
a.l <- 36.87 # the slope of the left bank [°]
a.r <- 78.69 # the slope of the right bank [°]
b.l <- a.l*pi/180 # the slope of the left bank [rad]
b.r <- a.r*pi/180 # the slope of the right bank [rad]
d90 <- 0.15 # diameter of the equivalent sand roughness reached by 90% of the blocks [m]
alpha <- 1.0 # the ratio of velocities between the one influenced by the walls and the bottom of the bed, (due to the variataion of roughness of the bed and the banks), if weak, put 1, if strong put 1.09 (because the max is 1.1 and we produce a random sample below)
n.m.l <- 0.0342 # Manning roughness near the left bank wall (same as 1/Strickler)
n.m.r <- 0.025 # Manning roughness near the right bank wall (same as 1/Strickler)

Computational workflow

The workflow presented here is the one developped by the ETHZ-VAW (Hydraulic lab in Zurich, Switezrland) and proposed in BEZZOLA (2011).

Make a first guess of the water depth h and add it to the variable

In [ ]:

# 2.Estimation of flow depth
h <- 4.5 #guess of the flow depth

Estimation hydraulic radius near the bed with this data it then possible to define the hydraulic radius R_s = 0.9 h.

Note the subscript "s" stand for "sole" the original German term for the river bed, by distinction from the walls denoted with the subscript "w"

In [ ]:

# 3.Estimation hydraulic radius and cross-section area
Rs <- 0.9*h
A <- 0.5*(h^2/tan(b.l))+h*Ps+0.5*(h^2/tan(b.r))
print(Rs)
print(A)

Estimation of the As area With the estimated value for R_s, the area A_s of the partial bed cross-section could be computed as A_s = R_s P_s.

In [ ]:

# 4. Computation of the area only influenced by the bed
As <- Rs*Ps
print(As)

The mean velocity throughsection may be computed (Um_s in m s^-1) using the logarithmic resistance law (which is more appropriate for river with high slope gradient, KEULEGAN, 1938).

\( Um_{s} = 2.5\log{\frac{12 R_{s}}{2 d_{90}}}*\sqrt{g R_{s} J}\)

where

R_s = the hydraulic radius (unit is m)
d₉₀ = the diameter of the equivalent sand roughness achieved by 90% of the blocks(unit is m)
g = gravitational acceleration = 9.81 m s^-2

In [ ]:

# 5.Calculation of the average velocity influenced by the bed with the steep slope log law
Ums <- 2.5*log((12*Rs)/(2*d90))*sqrt(g*Rs*J)
print(Ums)

Based on the velocity Um_s near the central part of the, the velocities Um_w near the wall influence areas are determined. There with

similar roughness for the bed and the banks \(Um_{w} ≈ Um_{s}\)
for greater differences in roughness, the assumption of equal velocities above the bed and in partial cross-sections near the wall is invalid and

\(Um_{w} = \frac{Um_{s}}{A - A_{s}} \left(\frac{A}{\alpha} - A_{s}\right) \)

where α can take values of up to 1.05 (or up to 1.1 for extreme roughness differences).

In [ ]:

# 6. Calcul of the average velocity along the wall
Umw <- Ums/(A-As)*((A/alpha)-As)
print(Umw)

With the approach developped by STRICKLER (1923), the hydraulic radius Rw_l and Rw_r for the left and right wall influenced areas are calculated (here for example on the left bank, therefore the subscript "l").
\(Rw_{l} = \left(\frac{Um_{w}}{m_{l}^{-1}\sqrt{J}}\right)^{3/2}\)

In [ ]:

# 7. Computation of the hydraulic radius near the wall following Strickler'equation
# 7.1 Left hydraulic radiu
Rw.l <- (Umw/((1/n.m.l)*sqrt(J)))^(3/2) 
# 7.2 Right hydraulic radiu
Rw.r <- (Umw/((1/n.m.r)*sqrt(J)))^(3/2)
print(Rw.l)
print(Rw.r)

With the wetted perimeter of the various partial cross-sections (P_s, P_w.l and P_w.r, see step 1), the hydraulic radii of the bottom partial cross-section R_s (step 2) and the wall influence areas R_w.i (step 7) it follows that A₁ is the sum of all partial areas.
\(A_{1} = A_{s} + \sum{A_{w.i}} = R_{s} P_{s} + \sum{P_{w.i} R_{w.i}}\)

This should correspond to the area avaialble for the flow defined by the total cross-section, i.e. it imply that

\(A_{1} = A\)

In [ ]:

# 8. Evaluation of the global area 

A1 <- As+(h/sin(b.l))*Rw.l+(h/sin(b.r))*Rw.r
print(A1)

It is now necessary to iteratively find the value for R_s for which the condition A1 = A is fulfilled. Normally, the calculation converges relatively quickly (it could be done manually), if for the second iteration the improved estimate for R_s is the previous value multiplied by the ratio A/A1. Thanks to "R" this optimization may be done automatically.

In [ ]:

# 9 Creating the function to be optimised A = A1
# As we are searching for a minimum therefore we have (A-A1)^2=0
Rsf <-function(x)((A)-(x*Ps+(h/sin(b.l))*Rw.l+(h/sin(b.r))*Rw.r))^2
Rsf.opt<-optimize(Rsf, interval = c(Rs*.1, 3*Rs))
curve(Rsf, from=Rs*0.1, to=2*Rs, xlab="Rs", ylab="(A-A1)^2" )
Rs.opt<-Rsf.opt$minimum

print(Rs.opt)

You can now compute the average velocity in the area only influenced by the bed using Rs.opt

In [ ]:

# 10.Compute the average velocity in the area influenced by the bed
Ums.opt <- 2.5*log((12*Rs.opt)/(2*d90))*sqrt(g*Rs.opt*J)
print(Ums.opt)

Using the basic relation relating the mass transfer per unit of time one can compute the partial discharge for all distinct areas of the cross-section.

In [ ]:

# 11. Compute the discharge in the area influenced by the bed and the one influenced by the wall
Qs <- Ums.opt*Rs.opt*Ps
Qw <- Ums.opt*((A/alpha)-Rs.opt*Ps)
print(Qs)
print(Qw)

Then you get the total discharge in m³/s corresponding to the value h you guessed at step 2.

The workflow must be iteratively repeated till you get the design discharge, the one you want to reach. Inversely you could enter the flow depth corresponding to the bankfull discharge case. If the discharge computed is smaller than the one you have chosen as the target value (assuming that it is issue from hydrological analysis), then it means that overflow and flooding will happen !

Note that recoding the different values produced during the procedure will provide you the rating curve for this section.

In [ ]:

Q = Qs+Qw
print (Q)